Claus Johansen, Sønderborg, Danemark, 2014-11-30 -> 2020-01-14

Problème d'Apollonius

0) Table des matières :

1) Préface

2) Apollonius

3) Le Problème

4) Formulation Initiale

5) Préparation

6) La solution générale

7) Toutes les solutions

8) Les ± Signes

9) Traitement postérieur

1) Préface

• Ceci est une méthode directe pour résoudre le Problème d'Apollonius, adapté à un tableur ou un langage de programmation.
• La méthode conduit à une numération rationnelle pour les 3 cercles donnés ainsi que les 8 cercles tangents potentiels.
• La méthode donne une explication des solutions doubles.
• La méthode permet d'obtenir des solutions exactes (pas nombre décimal arrondi).

2) Apollonius

Ce paragraphe est un extrait légèrement réarrangé de l'article de Wikipedia, complété par une traduction de l'anglais dito :

Apollonios de Perga ou Apollonius de Perge [Pergaeus] (en grec ancien : Άπολλώνιος) (v. 262 - v. 190 av J.-C.). Apollonius était un géomètre et astronome grec. Apollonios est célèbre pour ses écrits sur les sections coniques. C’est aussi lui qui donna à l’ellipse, à la parabole, et à l’hyperbole les noms que nous leur connaissons. Sa méthode novatrice et sa terminologie, spécialement dans le domaine des coniques, a influencé plusieurs mathématiciens postérieurs dont Klaudios Ptolemaios, Francesco Maurolico, Johannes Kepler, Isaac Newton, et René Descartes. On lui attribue en outre l’hypothèse des orbites excentriques pour expliquer le mouvement apparent des planètes et la variation de vitesse de la Lune. Le théorème d'Apollonius explique que le deux modèles sont équivalent donné les paramètres convenable. Ptolémée décrit ce théorème dans l'Almageste XII.1. Apollonius a aussi étudié l'histoire lunaire. Pour cela il est dit qu'il était appelé Epsilon (ε). Le cratère lunaire Apollonius fut baptisé ainsi en son honneur.

3) Le Problème

Trouvé les jusqu'à 8 cercles qui sont tangentes à 3 cercles donnés :

Fig. 1 : Le problème.

3.1) Commentaires

Le problème d'Apollonius a été initialement formulé comme un problème à la règle et au compas, et il existe des solutions de ce type. Mais montré ici est seulement une solution analytique simple.

Il existe également plusieurs solutions analytiques différentes. Celui montré ici est basée sur le théorème de Pythagore, d'autres utilisent la formule de Héron ou des principes totalement différents.

4) Formulation Initiale

En termes simples : Pour une solution analytique, la relation essentielle de tous les cercles donnés et n'importe quel cercle tangent (solution) doit être :

La distance entre les centres des cercle = La somme des rayons des cercle.

Quand cette relation est utilisée successivement pour tous les 3 cercles donnés, ça conduit à 3 équations :

Lorsque les 3 cercles donnés sont désignés A, B et C ayant les coordonnées des centres (s_A, t_A), (s_B, t_B) et (s_C, t_C) et les rayons r_A, r_B et r_C, une solution du problème, un cercle tangent au centre de (s₀, t₀) et rayon r₀, doit satisfaire à ces 3 équations :

		(4.1)
		(4.2)
		(4.3)

Où "-" dans le "±" indique que le cercle donné respective est circonscrit par le cercle tangent et vice versa.

Si les 3 équations sont élevés au carré pour se débarrasser des racines carrées, un peu maladroits, les équations générales deviennent :

		(4.4)
		(4.5)
		(4.6)

5) Préparation

La simplicité relative de cette solution dépend d'un positionnement bien choisi des 3 cercles donnés dans un système coordonné convenable :

Fig. 2 : Système coordonnées initial.	Fig. 3 : Système coordonnées transformé.

Le procédé peut être considéré comme une procédure en deux étapes :

1. Une rotation pour aligner l'axe x de deux centres des cercles, ici A et B.
2. Une translation x et y combiné pour faire l'axe x passe par les centres des deux cercles (ici A et B) et faire l'axe y passe par le centre du troisième cercle (ici C).

5.1) Rotation

Trouvez les distances des centres des cercles (A & B) :

		(5.1)
		(5.2)

Trouvez l'angle de rotation par ex. :

(5.3)

NB : Contrôlez l'usage de la fonction atan2. Montré ici comme atan2(y, x) mais souvent défini comme atan2(x, y).

Tournez les 3 coordonnées des centres au système coordonnées intermédiaire (u, v) par les formules générales :

		(5.4)
		(5.5)

5.2) Translation

Alignez le système coordonnées tourné (ou intermédiaire) (u, v) sur deux centres des cercles pour former le système coordonnées montré sur la fig. 3 (x, y). C'est simplement égal aux deux coordonnées des centres des cercles dans le système coordonnées tourné (ou intermédiaire) (u, v) :

		(5.6)
		(5.7)

Translatez le 3 coordonnées des centre sur le système coordonnées désiré (x, y) par les formules générales :

		(5.8)
		(5.9)

5.3) Effet

Les 3 équations de § 4, éq. 4.4, 4.5 et 4.6 vont maintenant prendre la forme :

Lorsque les 3 cercles donnés sont désignés A, B et C, ayant les coordonnées des centres (x_A, 0), (x_B, 0) et (0, y_C) et les rayons r_A, r_B et r_C, une solution du problème, un cercle tangent de centre (x₀, y₀) et de rayon r₀, doit satisfaire ce 3 équations :

		(5.10)
		(5.11)
		(5.12)

Si finalement il est implicite entendu, que le rayon des cercles donné peut avoir un signe, selon qu'ils sont circonscrites par le cercle tangent ou non, les signes de ±, un peu confusionnels, peuvent être omis. Les 3 équations peuvent alors s'écrire :

		(5.13)
		(5.14)
		(5.15)

Où un rayon de cercle donné négatif indique que le cercle donné respectif est circonscrit par le cercle tangent et vice versa.

C'est la solution de ces 3 équations qui est montré ci-dessous.

5.4) Commentaires

Le nombre des constantes dans les équations sont par cette procédure réduites de 9 à 6 :

• De : s_A, t_A, r_A, s_B, t_B, r_B, s_C, t_C, r_C
• À : x_A, r_A, x_B, r_B, y_C, r_C
• Comme : y_A = y_B = x_C = 0

Ce qui réduit considérablement la quantité de travail et la complexité !

Il y a 6 manières possibles de la transformation du système de coordonnées, dépendant de la séquence de numérotation des 3 cercles donné, mais ils conduisent finalement aux mêmes résultats :

Fig. 4 : Système de coordonnées possibles pour la transformation.

6) La solution générale

Soit :

		(6.01)
		(6.02)
		(6.03)
		(6.04)
		(6.05)
		(6.06)
		(6.07)
		(6.08)
		(6.09)
		(6.10)
		(6.11)

Et soit :

		(6.12)
		(6.13)
		(6.14)
		(6.15)
		(6.16)
		(6.17)
		(6.18)
		(6.19)
		(6.20)

Puis soit :

		(6.21)
		(6.22)
		(6.23)

Et plus soit :

		(6.24)
		(6.25)
		(6.26)

Finalement soit :

(6.27)

Ensuite, une solution générale au problème d'Apollonius, représenté par le rayon r₀ et les coordonnées du centre (x₀, y₀), peut être trouvé comme :

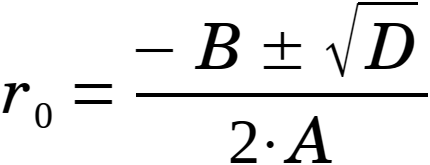		(6.28)
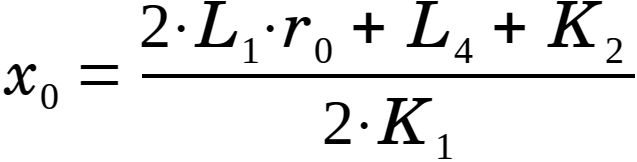		(6.29)
		(6.30)

6.1) Commentaires

Les équations sont assez robustes et donnent des solutions dans la plupart des cas. Certains des solutions proposées ne seront pas correctes et cela devrait être vérifié par exemple par comparer les distances des centres des cercles avec la somme des rayons - entièrement analogique à la façon dont les équations initiales ont été établies, cf. éq. 4.1 - 4.3, 4.4 - 4.6, 5.10 - 5.12 ou 5.13 - 5.15.

Les équations peuvent gérer les cercles donnés et cercles tangents à dégénérer en points, mais pas qu'ils dégénèrent en lignes droites.

Dans l'expression r₀ (éq. 6.28) D peut devenir négative.

Dans l'expression r₀ (éq. 6.28) A peut devenir nulle et ainsi conduire à un dénominateur égale à zéro.

7) Toutes les solutions

Les jusqu'à 8 solutions peuvent être obtenues en variant les signes des rayons des 3 cercle donné A, B et C. Si le rayon est positif, le cercle donné respective est placée en dehors du cercle tangent. Si le rayon est négatif, le cercle donné respective est placée à l'intérieur du cercle tangent.

Les solutions peuvent être numérotées comme :

Fig. 5 : Solutions transformées.

8) Les ± Signes

Il y a deux ± signes dans la solution :

8.1) La ± Signe dans la "r" équation (6.28)

La ± signe dans la "r" équation (6.28) prend soin des solutions doubles. Normalement, le signe "-" doivent être utilisés, mais dans certains cas spéciaux tous les deux signes peuvent être correctes. Un exemple est présenté ci-dessous.

Selon la numérotation présentée dans le tableau dans la section précédente, ces solutions sont désignés comme nº 4-, 4+, 5-, 5+ , 6-, 6+, 8- et 8+ :

Fig. 6 : Solutions doubles transformées.

8.2) Les ± signes dans la "y" équation (6.30)

Les deux signes peuvent être correctes individuellement et se produisent avec la même fréquence.

9) Traitement postérieur

Si le problème a d'abord été transformé d'un système de coordonnées (s, t) à un système de coordonnées (x, y) il peut être transformé en arrière. C'est les opérations inverses de la préparation au § 5 "Préparation" et les quantités la trouvé : Δu, Δv et α sera réutilisé ici.

9.1) Translation

Translatez les coordonnées des centres en arrière au système coordonnées intermédiaire (u, v) par les formules générales :

		(9.1)
		(9.2)

9.2) Rotation

Tournez les coordonnées des centres en arrière au système coordonnées initiales (s, t) par les formules générales :

		(9.3)
		(9.4)

Fig. 7 : La solution.