
Claus Johansen, Sønderborg, Denmark, 2014-11-30 -> 2020-01-14
| Overview |
0) Contents:

|

|

|

|

|

|

|

|
This paragraph is a slightly rearranged extract of the Wikipedia article:
Wikipedia, the free encyclopedia|
Apollonius of Perga [Pergaeus] (Ancient Greek: Άπολλώνιος) (c. 262 BC - c. 190 BC). Apollonius was a Greek geometer and astronomer noted for his writings on conic sections. His innovative methodology and terminology, especially in the field of conics, influenced many later scholars including Ptolemy, Francesco Maurolico, Johannes Kepler, Isaac Newton, and René Descartes. It was Apollonius who gave the ellipse, the parabola, and the hyperbola the names by which we know them. The hypothesis of eccentric orbits, or equivalently, deferent and epicycles, to explain the apparent motion of the planets and the varying speed of the Moon, is also attributed to him. Apollonius' theorem demonstrates that the two models are equivalent given the right parameters. Ptolemy describes this theorem in the Almagest XII.1. Apollonius also researched the lunar history, for which he is said to have been called Epsilon (ε). The crater Apollonius on the Moon is named in his honour. |

|

|

|

|

|
Find the up to 8 circles that are tangents to 3 given circles:
|
|
| Fig. 1: The problem. |
Apollonius' Problem was initially formulated as a classical compass and straightedge problem and there exist some solutions of this type. But shown here is only a simple analytical solution.
There exist also several different analytical solutions. The one shown here is based on the Pythagorean formula, others uses Heron's Formula or completely different principles.

|

|

|

|
In plain words: For an analytical solution, the key relationship of all given circles and any tangent circle must be:
The distance between circle centres = Sum of circle radii.
When this relationship is used successively for all 3 given circles it leads to 3 equations:
If the 3 given circles are denoted A, B and C with the centre coordinates (sA, tA), (sB, tB) and (sC, tC) and the radii rA, rB and rC then a solution to the problem, a tangent circle with centre at (s0, t0) and radius r0 must satisfy these 3 equations:
| (4.1) | ||
| (4.2) | ||
| (4.3) |
Where "-" in the "±" indicates that the respective given circle is circumscribed by the tangent circle and vice versa.
If the 3 equations are squared to get rid of the somewhat awkward square roots, the general equations look like:
| (4.4) | ||
| (4.5) | ||
| (4.6) |

|

|

|

|
The relative simplicity of the solution relies on a well-chosen positioning of the 3 given circles in a convenient coordinate system:
|
|
|
| Fig. 2: Initial coordinate system. | Fig. 3: Transformed coordinate system. |
The process can be seen as a two-step procedure:
Find the centre coordinate distances (A & B):
| (5.1) | ||
| (5.2) |
Find the angle of rotation by e.g.:
| (5.3) |
NB: Check the use of the atan2-function. Shown here as atan2(y, x) but is often defined as atan2(x, y).
Rotate the 3 centre coordinates to the intermediate coordinate system (u, v) by the general formulas:
| (5.4) | ||
| (5.5) |
Align the rotated coordinate system (u, v) with two circle centres to form the coordinate system shown in fig. 3 (x, y). It's simply equal to two circle centre coordinates in the rotated coordinate system (u, v):
| (5.6) | ||
| (5.7) |
Translate the 3 centre coordinates to the desired coordinate system (x, y) by the general formulas:
| (5.8) | ||
| (5.9) |
The 3 equations from § 4, eq. 4.4, 4.5 and 4.6 will now take the form:
When the 3 given circles are denoted A, B and C with the centre coordinates (xA, 0), (xB, 0) and (0, yC) and the radii rA, rB and rC then a solution to the problem, a tangent circle with centre at (x0, y0) and radius r0 must satisfy these 3 equations:
| (5.10) | ||
| (5.11) | ||
| (5.12) |
If finally it's implicit understood, that the given circles radius can have a sign, depending on whether they are circumscribed by the tangent circle or not, the somewhat confusing ± signs can be omitted. The 3 equations can then be written as:
| (5.13) | ||
| (5.14) | ||
| (5.15) |
Where a negative given circle radius indicates that the respective given circle is circumscribed by the tangent circle and vice versa.
It's the solution of these 3 equations that is shown below.
The number of constants in the equations is by this procedure reduced from 9 to 6:
This reduces the amount of work and the complexity considerably!
There are 6 possible ways of transforming the coordinate system, depending on the numbering sequence of the 3 given circles, but they will in the end all lead to the same results:
|
|
| Fig. 4: Possible coordinate systems for transformation. |

|

|

|

|
Let:
| (6.01) | ||
| (6.02) | ||
| (6.03) | ||
| (6.04) | ||
| (6.05) | ||
| (6.06) | ||
| (6.07) | ||
| (6.08) | ||
| (6.09) | ||
| (6.10) | ||
| (6.11) |
And let:
| (6.12) | ||
| (6.13) | ||
| (6.14) | ||
| (6.15) | ||
| (6.16) | ||
| (6.17) | ||
| (6.18) | ||
| (6.19) | ||
| (6.20) |
Then let:
| (6.21) | ||
| (6.22) | ||
| (6.23) |
Further let:
| (6.24) | ||
| (6.25) | ||
| (6.26) |
Finally let:
| (6.27) |
Then a general solution to Apollonius' Problem, represented by the radius r0 and centre coordinates (x0, y0) can be found as:
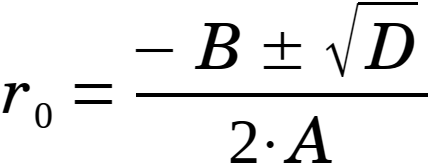 |
(6.28) | |
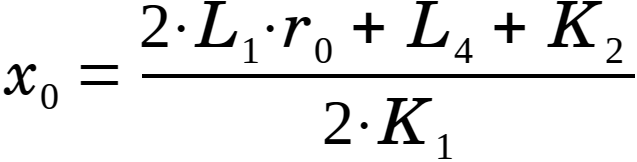 |
(6.29) | |
| (6.30) |
The equations are quite robust and will give solutions in most cases. Some of the proposed solutions will not be correct and this should be checked e.g. by comparing the centre distances of the circles with the sum of radii - fully analogue to the way the Initial equations were established, cf. eq. 4.1 - 4.3, 4.4 - 4.6, 5.10 - 5.12 or 5.13 - 5.15.
The equations can handle the given circles and tangent circles to degenerate into points but not that they degenerate into straight lines.
In then r0 expression (eq. 6.28) D can become negative.
In then r0 expression (eq. 6.28) A can become zero and thereby lead to a zero denominator.

|

|

|

|
The up to 8 solutions can be obtained by varying the sign of the 3 given circle radii A, B and C. If the radius is positive, the respective base circle is placed outside the tangent circle. If the radius is negative, the respective given circle is placed inside the tangent circle.
The solutions can be numbered as:
| No | rA | rB | rC |
| 1 | + | + | + |
| 2 | - | + | + |
| 3 | + | - | + |
| 4 | + | + | - |
| 5 | + | - | - |
| 6 | - | + | - |
| 7 | - | - | + |
| 8 | - | - | - |
|
|
| Fig. 5: Transformed solutions. |

|

|

|

|
There are two ± signs in the solution:
The ± signs in the "r" equation (6.28) take care of double solutions. Normally the "-" sign should be used, but in some special cases both signs can be correct. One example is shown below.
According to the numbering presented in the table in the previous section, these solutions are designated as no 4-, 4+, 5-, 5+ , 6-, 6+, 8- and 8+:
|
|
| Fig. 6: Transformed double solutions. |
Both signs can be correct individually and occur with same frequency.

|

|

|

|
If the problem was initially transformed from a (s, t) coordinate system to a (x, y) coordinate system, the solution can be transformed back. It's the reverse operations of the preparation in § 5 "Preparation" and the properties found there: Δu, Δv and α will be re-used here.
Translate the centre coordinates back to the intermediate coordinate system (u, v) by the general formulas:
| (9.1) | ||
| (9.2) |
Rotate the centre coordinates back to the initial coordinate system (s, t) by the general formulas:
| (9.3) | ||
| (9.4) |
|
|
| Fig. 7: The solution. |

|

|

|

|
| Overview |